La solución al enigma electoral

Si llamamos x al número de votos obtenidos por el partido más votado, y teniendo en cuenta el enunciado, llegamos a que

x+(x-214)+(x-317)+(x-318)=1425. Resolviendo esa ecuación obtenemos que el partido más votado recibió 586 votos y los demás 372, 269 y 208.

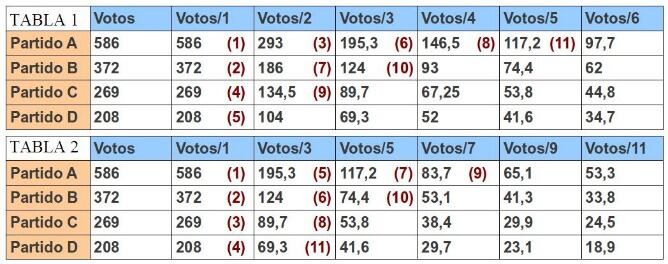
La legislación española efetúa el reparto de escaños mediante la ley de D'Hondt, que implica dividir el número de votos obtenidos por cada partido entre 1,2,3,4,5, ... tal como se hace en la primera tabla.

Los concejales a asignar corresponden a los números mayores en esa tabla. Así el primer concejal corresponde al partido A (586), el segundo a B (372), el tercero a A (293), y siguen C, D, A, B, A, C, B, A (en rojo, entre paréntesis, aparece el orden de consecución de concejales).

La solución es que corresponden 5 concejales a A, 3 a B, 2 a C y 1 a D.

Algunos oyentes daban como solución 4 concejales para A, 3 para B, 2 para C y 2 para D. Eso sería correcto si en España se utilizase el método de Sainte-Laguë en lugar del método de D'Hondt. Este método es similar, pero en vez de dividir los votos obtenidos por 1,2,3, 4 ... se dividen por números impares: 1,3,5,7,... Con esa regla, el resultado de la elección, sería el planteado en la segunda tabla

Estos métodos han pasado a la historia con los nombres de D'Hondt y Saint-Laguë, aunque son equivalentes a otros diseñados por Thomas Jefferson y Daniel Webster, respectivamente, que se utilizaron con anterioridad en el sistema electoral de Estados Unidos.