Lo que PISA no cuenta
Se trata de una de las pruebas educativas más influyentes del mundo. Sin embargo, está mostrando muchos puntos débiles. Antes de las irregularidades que se han descubierto hace unas semanas en España, varios grupos de investigadores como este de la Universidad de Oviedo ya habían estudiado la poca fiabilidad de estas pruebas

Un objetivo básico de la evaluación PISA es que sus instrumentos de medida sean aplicables y válidos en contextos culturales diferentes / GETTY IMAGES

Oviedo
PISA evalúa las habilidades de los estudiantes de 15 años en Lectura, Matemáticas y Ciencias cada tres años y establece un ranking de países según el rendimiento en cada competencia.
En las primeras ediciones, Finlandia ocupó el puesto número uno, pero en las últimas dio paso a Shanghái (China), Singapur y Hong-Kong, con sistemas educativos muy diferentes. Esto muestra que “copiar” los métodos de educación sin tener en cuenta las características culturales de cada país no garantiza una mejora.
A pesar de la enorme influencia de PISA en la educación, existen críticas muy fundadas sobre su funcionamiento.
A continuación, se muestran algunos puntos débiles de PISA con ejemplos referidos a temas que la propia evaluación considera muy importantes y cuya detección resulta bastante obvia:
Enunciados inadecuados
Para medir la oportunidad de aprender, PISA plantea preguntas sobre conceptos matemáticos como “ecuación lineal” o “vectores”, y el alumno debe elegir su respuesta entre las opciones:
1) No lo he visto nunca.
2) Lo he visto una o dos veces.
3) Lo he visto varias veces.
4) Lo he visto a menudo.
5) Lo conozco bien, entiendo el concepto.
¿A qué opción debe responder un alumno al que le hayan explicado el concepto varias veces y que lo entienda bien? En consecuencia, las conclusiones de analizar las respuestas a este ítem, ¿se refieren a lo que los alumnos creen que saben o a su exposición/conocimiento de los conceptos?
Sesgo cultural
Un objetivo básico de la evaluación PISA es que sus instrumentos de medida sean aplicables y válidos en contextos culturales diferentes. En 2012, para evaluar la familiaridad con conceptos matemáticos incluyó trece reales y tres falsos: “número genuino”, “fracción declarativa” y “escala subjuntiva”. Esto posibilitó usar la técnica de preguntas trampa y elaborar el índice corregido FAMCONC (familiaridad con los conceptos matemáticos).
En contra de lo esperado, la relación de FAMCONC con las Matemáticas es muy distinta al agrupar los países por zonas geográfico-culturales. En la gráfica 1 se muestran por un lado el conjunto de países europeos o anglosajones y, por otro, el resto de países.

Gráfica 1. Relación entre FAMCONC y Matemáticas según la zona geográfica y cultural de los países. / THE CONVERSATION
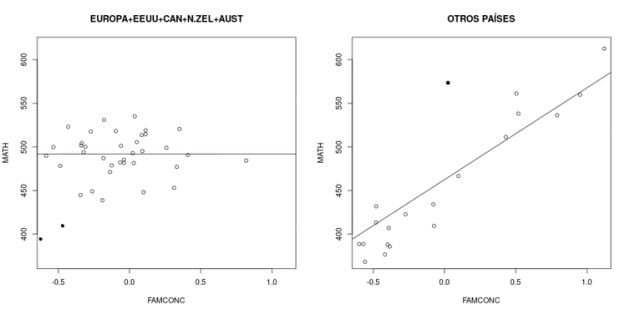
Gráfica 1. Relación entre FAMCONC y Matemáticas según la zona geográfica y cultural de los países. / THE CONVERSATION
Si el sesgo cultural se hubiese eliminado las dos gráficas serían similares, pero en Europa y los países con cultura anglosajona FAMCONC y Matemáticas son independientes, mientras que en el resto la relación es creciente y muy fuerte.
Curiosamente, PISA no hace referencia alguna a estos problemas, ni empleó en 2015 estas técnicas de corrección.
Cambios en los cuestionarios y seguimiento de resultados
PISA señala la importancia de analizar la evolución temporal de sus indicadores. Sin embargo, son frecuentes los cambios en los enunciados y las definiciones de los índices, sin que se explique la causa.
Un ejemplo de esta situación se produjo al estudiar la relación de la Enseñanza Dirigida por el Docente (EDD) con el rendimiento (en este estilo docente priman las clases magistrales, frente a la Enseñanza Basada en la Investigación, caracterizada por trabajo por proyectos, por ejemplo). En 2012, se empleó un cuestionario para Matemáticas y otro muy diferente en 2015 para Ciencias. Ambos eran generales y sin preguntas específicas ni de Ciencias ni de Matemáticas.
Por otro lado, en 2012 la relación de EDD en Matemáticas con el rendimiento en esta materia es casi idéntica a la que tiene con Ciencias y Lectura; en 2015 ocurre lo mismo con la EDD de Ciencias (ver la gráfica 2 para Ciencias y Matemáticas). Este resultado es sorprendente porque las tres materias se imparten de manera independiente, lo que plantea dudas sobre qué mide el índice que PISA define para cuantificar la EDD.
En la gráfica 3 se observan los cambios de signo de 2015 respecto a 2012, que afectan a la gran mayoría de los países (puntos rojos), de la correlación de EDD con las Matemáticas y Ciencias.

Gráfica 2. Relación entre Ciencias y Matemáticas en 2012 y 2015. / THE CONVERSATION
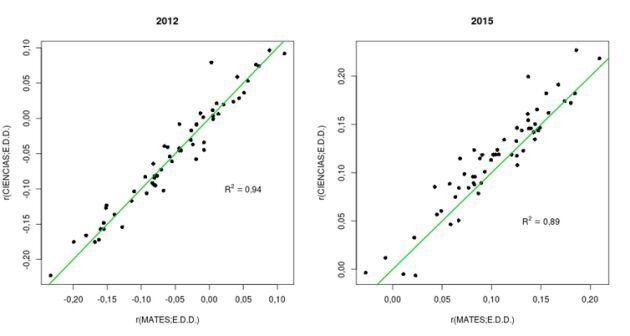
Gráfica 2. Relación entre Ciencias y Matemáticas en 2012 y 2015. / THE CONVERSATION
Dados la modificación de los cuestionarios, el cambio de signo en las correlaciones y la ausencia de especificidad de EDD, ¿qué fiabilidad puede darse a las conclusiones de PISA sobre este tema?

Gráfica 3. Cambio en la relación de Matemáticas y EDD de 2012 a 2015. / THE CONVERSATION
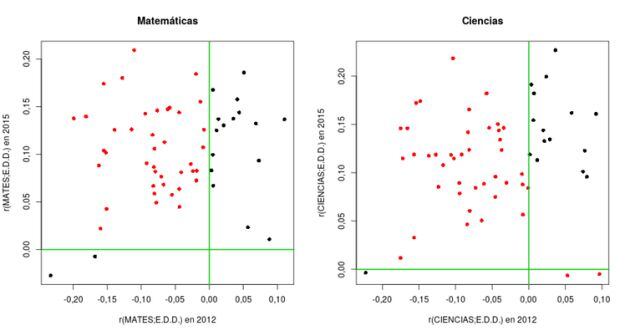
Gráfica 3. Cambio en la relación de Matemáticas y EDD de 2012 a 2015. / THE CONVERSATION
Cómo aborda PISA los resultados inesperados
Un aspecto fundamental en una investigación es detectar los resultados inesperados y dar una explicación coherente y bien fundamentada. Sin embargo, es muy frecuente que ante este tipo de situaciones PISA recurra a generalidades o explicaciones sin base en los datos del estudio.
Por ejemplo, en la edición del año 2015 PISA compara la relación de las Matemáticas con las metodologías de enseñanza: la dirigida por el docente (EDD) y la basada en la investigación (EBI). En sus resultados obtiene una correlación de +0,31; cabría esperar, no obstante, que fuera negativa pues tales metodologías son casi contrapuestas: si un 70 % del tiempo de trabajo en el aula lo hacen los estudiantes, las explicaciones magistrales del docente se reducen a un 30 %, y viceversa.
PISA explica este hecho señalando que hay una correlación débil entre ellas y se pregunta a qué dedican las horas de clase los estudiantes con valores bajos en las dos metodologías. Ambas afirmaciones son vagas e insuficientes. En cualquier caso, PISA detecta el problema pero no estudia el origen ni las implicaciones de este resultado.
Otro resultado inesperado es la relación negativa de la EBI con el rendimiento. Según PISA, esta metodología es muy importante ya que los estudios previos indican que puede mejorar el aprendizaje y la adquisición de destrezas como el razonamiento crítico. Sin embargo, sus resultados van en otra dirección pues la EBI tiene relación negativa con Matemáticas en 56 países.
Los comentarios de PISA para explicar este hecho son:
- El laboratorio solo mejora el aprendizaje si los estudiantes realizan actividades manuales y manejan conceptos.
- El tiempo dedicado a los laboratorios se emplea de manera ineficiente.
- En ocasiones las actividades manuales se utilizan para hacer más atractiva la ciencia a los estudiantes con problemas.
- Los estudiantes solo trabajan realmente cuando hay buen material y el profesor está bien formado.
Estas explicaciones carecen de validez por varias razones:
- Los resultados son idénticos para Lectura y Matemáticas, que nada tienen que ver con los laboratorios de ciencias.
- La buena formación del profesorado y la calidad del material son aplicables a cualquier método de enseñanza.
- Claramente PISA evita un análisis profundo para detectar las causas de este resultado, como comprobar la representatividad del indicador que usa para cuantificar la EBI.
En resumen, la fiabilidad de las conclusiones de PISA ha de ponerse en entredicho por:
- Los errores en la elaboración de los cuestionarios.
- El sesgo cultural que no han sido capaces de eliminar.
- Resultados contradictorios y dificultades para el seguimiento longitudinal.
- Explicaciones superficiales ante resultados inesperados.
Norberto Corral Blanco, Catedrático de Universidad. Área de Estadística e Investigación Operativa, Universidad de Oviedo; Carlos Carleos Artime, profesor en el departamento de Estadística e Investigación Operativa y Didáctica de la Matemática, Universidad de Oviedo y Sara Álvarez Morán, Profesora en el departamento de Estadística e Investigación Operativa y Didáctica de la Matemática, Universidad de Oviedo
Este artículo fue publicado originalmente en The Conversation. Lea el original.





